![[ Genetic Algorithm ] 유전 알고리즘을 통해 비밀번호를 뚫어보자!](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcQnr1u%2FbtrnWSkim4h%2FqwH9ybFRFzfi6OuenTrtw1%2Fimg.png)
이번 포스팅에서는 유전 알고리즘을 통해 비밀번호를 찾는 알고리즘이다.
그전에 유전 알고리즘에 대해서 간략하게 설명을 하자면 다음과 같다.
말 그대로 유전 즉, 세대가 존재한다는 뜻이다. 이게 무슨 뜻이냐...
우선 랜덤으로 최초의 아이들을 생성한다.
그리고 그 생성된 아이들을 가지고 fitness (성능)을 측정한다.
성능을 측정할 때 적절한 점수를 부여하여 만약 점수가 높다면 해당 아이들을 선발해 낸다.
그리고 선발된 아이들을 교배하여 다음 세대를 만들어낸다.
그 과정에서 돌연변이도 추가하여 다음 세대를 만들어 내고 또 태어난 자식들을 가지고 성능을 측정하여
위의 과정을 계속 반복하여 수 세대를 걸쳐서 답을 도출해 내는 것이 유전 알고리즘이다.
그렇다면 파이썬으로 유전 알고리즘을 구현해보자.
함수가 많아서 함수 하나하나씩 잘라서 설명을 해보려고 한다.
우선 비밀번호는 문자열을 사용하고 길이가 최소 2 ~ 최대 10 정도로 적당하게 설정한다.
그리고 랜덤으로 아스키코드의 문자와 숫자를 생성해야 하기 때문에 random과 string을 import 한다.
import random
import string
다음은 비밀번호를 길이만큼 랜덤으로 생성하는 함수이다.
def generate_word(length):
result = ""
x = "".join(random.sample(string.ascii_letters + string.digits, k=length))
return x입력값으로 비밀번호의 length를 받아와서 초기 result 값을 빈 문자열로 초기화 한 뒤에
random을 통해서 a~Z까지 0~9에 해당하는 임의의 아스키 문자와 숫자를 길이만큼 조합하여
x에 저장한 후 해당 비밀번호를 리턴해 준다.
print(generate_word(length=10)) // 길이가 10인 임의의 문자열 생성위와 같이 테스트를 해보면 결과는 다음과 같이 길이가 10인 숫자와 문자가 랜덤으로 생성된 것을 볼 수 있다.
다음으로 첫 세대를 만들어 보자.
// 첫번째 세대가 태어남.
def generate_population(size, min_len, max_len):
population = [] // 빈 리스트 생성
for i in range(size): // size 만큼 loop를 돌면서
// 최소 길이부터 최대 길이까지 밸런스하게 랜덤으로 생성한다.
length = i % (max_len - min_len + 1) + min_len
population.append(generate_word(length))
return population// 최소길이가 2이고 최대길이가 10인 문자열을 100개 생성
min_len = 2
max_len = 10
pop = generate_population(size=100, min_len=min_len, max_len=max_len)
print(pop)위와 같이 테스트를 진행하여 첫 번째 세대를 찍어보면 결과는 다음과 같다.
길이도 각자 다 다르고 숫자와 문자가 잘 섞인 것을 볼 수 있다.
이렇게 만들어진 세대를 가지고 fitness를 측정한다.
// fitness 측정 (성능 측정 단계)
def fitness(password, test_word):
score = 0 // 초기 점수는 0점으로 초기화.
// 길이가 다르면 0점 return
if len(password) != len(test_word):
return score
// 길이가 같으면 0.5점을 더해준다.
len_score = 0.5
score += len_score
// 설정한 비밀번호와 비교하여 해당 문자열이 있는지 있으면 1점을 더해준다.
for i in range(len(password)):
if password[i] == test_word[i]:
score += 1
// 백점 만점에 몇점인지 계산한다. (성능 측정)
return score / (len(password) + len_score) * 100위에서 생성한 비밀번호들을 가지고 초기에 점수를 0으로 초기화 한 뒤 우리가 설정한 비밀번호 password와 test_word를 비교하여 성능을 측정하면 결과로 100점 만점에 몇 점인지 그 비밀번호의 점수가 리턴 된다.
처음 분기문에서 비밀번호의 길이 자체가 다르면 다른 비밀번호이기 때문에 그냥 0점을 반환해버린다.
그런데 만약 test_word와 비밀번호의 길이가 같다면 0.5점을 더해준다.
그리고 그 아래 반복문에서는 비밀번호와 직접 요소 하나하나를 돌면서 문자열이 있으면 1점을 계속 더해준다.
그렇게 해서 성능이 측정되어진다.
실제로 어떻게 측정이 되는지 테스트를 해보자.
print(fitness('abcdE', 'abcde')) // 설정한 비밀번호와 비교하였을 때 점수는 81.81점)이렇게 함수를 호출하면서 첫 번째 인자에는 우리가 설정한 비밀번호, 두 번째 인자로는 test_word인
예측한 비밀번호가 들어가게 된다. 그럼 결과는 81.81점이 나온다.
다음으로는 compute_performance라는 함수이다.
이 함수는 위에서 만든 성능 측정 함수를 이용하여 태어난 자식들의 점수를 측정하여 비밀번호의 길이를 예측하는 함수이다. 그리고 점수를 내림차순으로 정렬한다.
def compute_performance(population, password):
performance_list = [] // population을 점수 순서대로 정렬하기 위해서 list 생성.
for individual in population:
// 각각의 자식들의 점수를 측정한다.
score = fitness(password, individual)
// 비밀번호의 길이를 예측할 수 있다.
if score > 0: // 점수가 0보다 크다는 뜻은 비밀번호의 길이는 맞췄다는 의미이다.
pred_len = len(individual) // 예상 길이를 pred_len 변수에 저장한다.
performance_list.append([individual, score])
// list를 정렬하는데 key(점수)를 기준으로 내림차순으로 정렬한다.
population_sorted = sorted(performance_list, key=lambda x: x[1], reverse=True)
return population_sorted, pred_len반환 값으로는 점수로 정렬된 아이들의 리스트와 비밀번호의 예상 길이가 리턴 된다.
다음 함수는 이렇게 계산된 아이들 중 살아남을 아이들을 선택하는 함수이다.
// 살아남은 아이들을 select할 함수이다.
def select_survivors(population_sorted, best_sample, lucky_few, password_len):
next_generation = []
// best_sample 수 만큼 뽑아서 다음 세대로 보낸다.
for i in range(best_sample):
if population_sorted[i][1] > 0:
next_generation.append(population_sorted[i][0])
// 랜덤으로 운이 좋은 자식들을 살린다.
lucky_survivors = random.sample(population_sorted, k=lucky_few)
for I in lucky_survivors:
next_generation.append(I[0])
// 다음 세대의 아이들의 수가 부족할 수 있기 때문에 랜덤으로 생성하여 채워넣는 부분이다.
if len(next_generation) < best_sample + lucky_few:
next_generation.append(generate_word(length=password_len))
// 다음 세대의 아이들 리스트를 랜덤한 순으로 섞는다.
random.shuffle(next_generation)
return next_generation위의 두 함수를 아래의 코드로 테스트해보자.
password = generate_word(length=10) // 길이가 10인 임의의 문자열 생성
print("password is ", password)
// 최소길이가 2이고 최대길이가 10인 문자열을 100개 생성
min_len = 2
max_len = 10
pop = generate_population(size=100, min_len=min_len, max_len=max_len)
pop_sorted, pred_len = compute_performance(pop, password)
print(pop_sorted)
// 100명의 자식들 중에서 성능이 우수한 20명과 운이 좋은 20명을 선발한다.
survivors = select_survivors(pop_sorted, best_sample=20, lucky_few=20, password_len=pred_len)
print('password length must be %s' % pred_len)
print(survivors)
가장 첫 줄에 비밀번호가 생성되고
다음 리스트에는 비밀번호의 길이를 맞춘 아이들이 보이고 해당 점수가 높은 아이들부터 정렬되는 것이 보인다. 첫 세대에 14점이나 획득했다는 것을 알 수 있다.
그리고 이를 통해서 비밀번호가 10자리 인 것도 알아냈다.
그리고는 살아남은 아이들에 대한 결과가 출력되어진 것을 볼 수 있다. 보면 아예 터무니없는 아이들이 거의 사라진 결과를 알 수 있었다.
다음 함수는 위의 마지막 결과처럼 살아남은 아이들을 가지고 교배시키는 함수이다.
// Create Children (살아남은 아이들을 교배시킨다.)
// individual1 : 엄마
// individual2 : 아빠
def create_child(individual1, individual2):
child = ''
// 더 짧은 길이의 유전자에 맞춰서 생성.
min_len_ind = min(len(individual1), len(individual2))
for i in range(min_len_ind):
if (int(100*random.random()) < 50): // 50%의 확률로 엄마의 유전자를 획득
child += individual1[i]
else:
child += individual2[i] // 나머지 50% 확률로 아빠의 유전자를 획득
return child
def create_children(parents, n_child):
next_population = []
for i in range(int(len(parents)/2)):
for j in range(n_child):
next_population.append(create_child(parents[i], parents[len(parents) -1 -i]))
return next_population살아남은 아이들을 가지고 적절히 나눠 가지면서 새로운 아이들을 만들어 낸다. 그리고 만들어낸 아이들을 다음 세대로 보내는 과정이다.
위의 함수를 테스트하여 자식들을 출력해 보자.
// survivors : 성능이 좋은아이들 20명, 운이좋은 아이들 20명 이므로 길이는 40
// 살아남은 아이들이 각각 5명씩 아이를 낳는다.
// 40명의 부모 = 20커플
// 5명씩 아이를 낳으면 20 X 5 = 100명
children = create_children(survivors, 5)
print("---------------children---------------\n", children)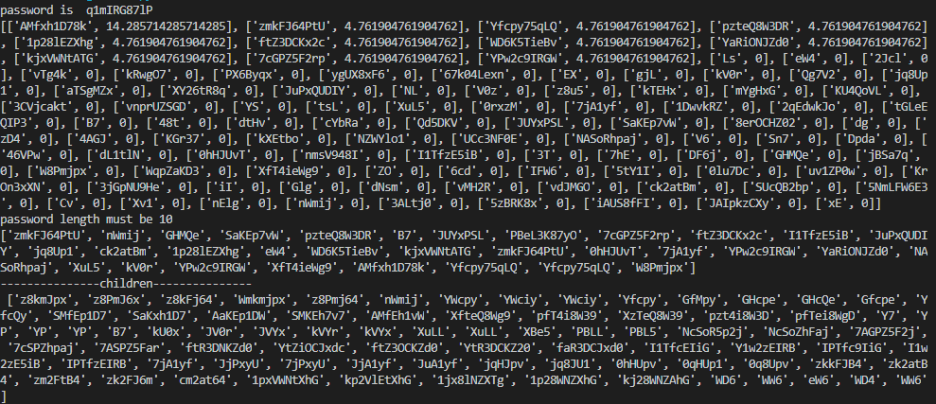
구분선을 추가하여 좀 보기 쉽게 출력해 보았다.
다음 함수로는 돌연변이를 생성하여 다음 세대에 추가하는 함수이다. 이 돌연변이를 통해서 비밀번호의 예측을 한 번에 끌어올릴 수 있도록 한다.
// 돌연변이 생성
def mutate_word(word):
// 비밀번호에서 임의의 idx 값을 추출한다
idx = int (random.random() * len(word))
// 추출한 idx 값에 랜덤한 값을 넣는다.
if (idx == 0):
word = random.choice(string.ascii_letters + string.digits) + word[1:]
else:
word = word[:idx] + random.choice(string.ascii_letters + string.digits) + word[idx+1:]
return word
// 100명의 아이들 중에서 10% 확률로 돌연변이를 생성한다.
def mutate_population(population, chance_of_mutation):
for i in range(len(population)):
if random.random() * 100 < chance_of_mutation:
population[i] = mutate_word(population[i])
return population
위의 함수들을 가지고 이제 메인에서 내가 비밀번호를 설정하고 옵션들을 설정하여 몇 세대만에 내가 설정한 비밀번호를 맞추는지 알아보자.
if __name__ == "__main__":
// 비밀번호의 최대, 최소 자릿수를 지정해놓음.
password = 'T4As2Dc39i'
min_len = 2
max_len = 10
n_generation = 300
population = 100
best_sample = 20
lucky_few = 20
n_child = 5
chance_of_mutation = 10
pop = generate_population(size=population, min_len=min_len, max_len=max_len)
// 총 300 세대를 생성하면서 반복한다.
for g in range(n_generation):
pop_sorted, pred_len = compute_performance(population=pop, password=password)
// pop_sorted에서 첫 번째의 점수가 100점이면 비밀번호 찾음.
if int(pop_sorted[0][1]) == 100:
print("SUCCESS! The password is %s" % (pop_sorted[0][0]))
break
survivors = select_survivors(population_sorted=pop_sorted, best_sample=best_sample, lucky_few=lucky_few, password_len=pred_len)
children = create_children(parents=survivors, n_child=n_child)
new_generation = mutate_population(population=children, chance_of_mutation=chance_of_mutation)
pop = new_generation
print("===========%sth generation==========" %(g+1))
print(pop_sorted[0])출력 결과로는 항상 가장 점수가 높은 아이만 출력하고 그 아이의 점수와 그 아이가 몇 세대인지만 출력해서 결과를 보면 아래와 같다.
총 237 세대만에 내가 초기에 설정한 비밀번호를 맞춰낸 모습을 볼 수 있다!
그렇지만, 실제로 이 알고리즘으로 비밀번호를 찾아낸다면?
최대 횟수 제한이 걸려있으므로 절~~ 대 불가능하다!
'✏️ PS > 알고리즘 이론' 카테고리의 다른 글
| [ Rotate Matrix ] 2차원 배열 회전 알고리즘 (0) | 2021.12.20 |
|---|---|
| [ Average Filter ] 실시간으로 들어오는 데이터의 평균을 구해보자! (2) | 2021.12.08 |
